Log の 微分 例題

いわんや 悪人 を や【logの微分】例題を解説!分数、合成関数はどうやる？ | 数スタ. log微分の例題解説! 対数微分法を用いた例題. まとめ. log微分の例題解説! 次の関数を微分せよ。 y = log 3x. 〈解答〉. y′ = (3x)′ 3x = 3 3x = 1 x. 別解として. y = log 3x = log 3 + log x. このように分けてから微分する方法もあります。 y′ = 0 + 1 x = 1 x. 次の関数を微分せよ。 y = log(x2 + 1) 〈解答〉. y′ = (x2 + 1)′ x2 + 1 = 2x x2 + 1. 分数の形を作る ⇒ 真数の微分を掛ける. この手順でOKですね! 次の関数を微分せよ。 y = log2 |2x|. 指数，対数関数の微分 | おいしい数学. 対数関数 から微分を考え，それに伴い登場する e の定義を紹介します．. 目次. 1： 指数・対数関数の微分公式. 2： 対数関数の微分と e の定義登場. 3： 例題と練習問題. 指数・対数関数の微分公式. 指数，対数関数の微分. a > 0 ， a ≠ 1 のとき. (ⅰ) (ax) ′ = axloga. ↓ 特に a = e. (ⅱ) (ex) ′ = ex. (ⅲ) (logax) ′ = 1 xloga. (loga | x |) ′ = 1 xloga. ↓ 特に a = e.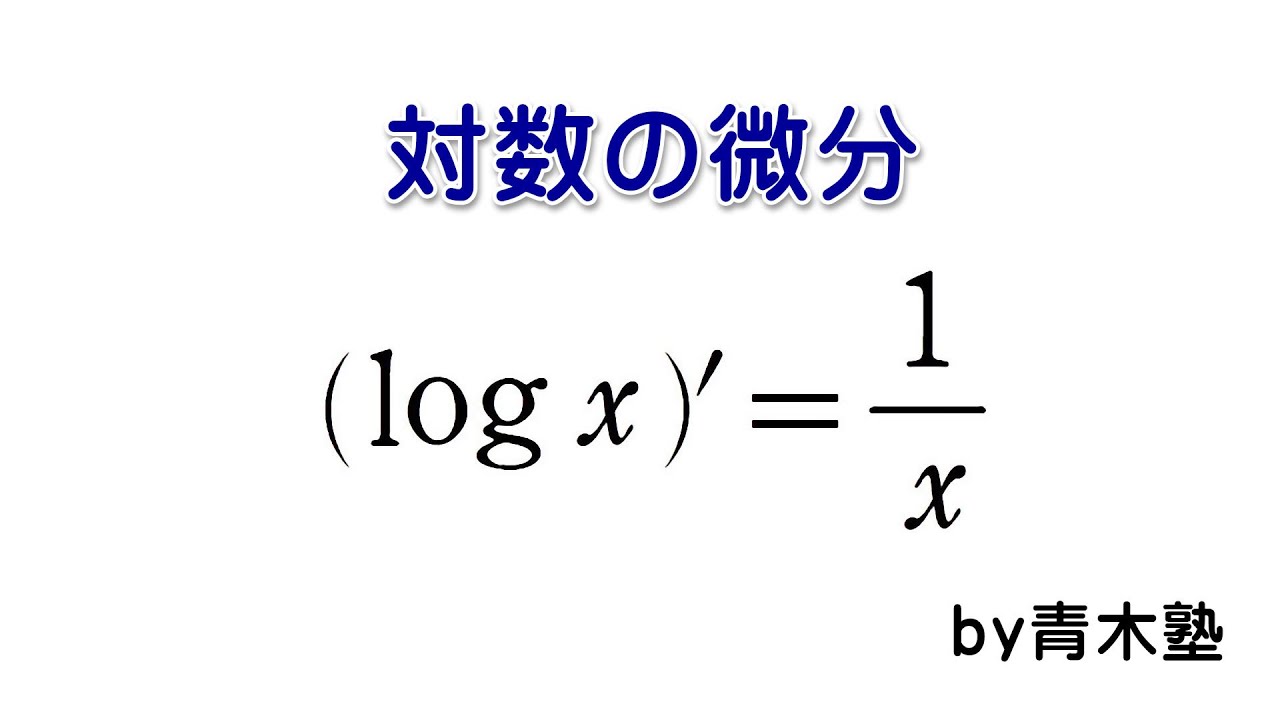

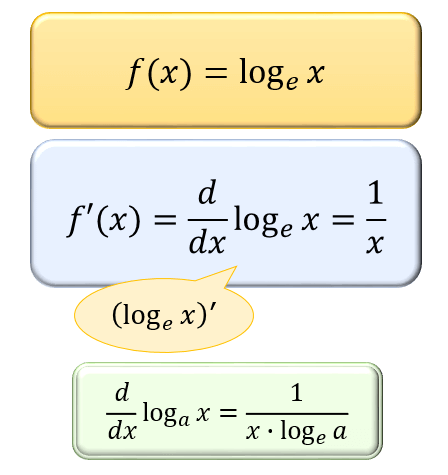
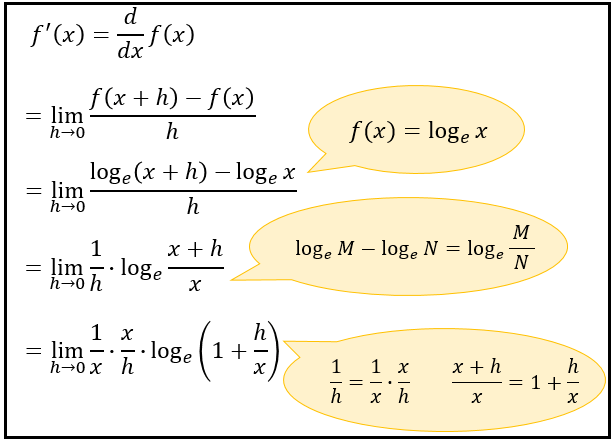
(ⅳ) (logx) ′ = 1 x. (log | x |) ′ = 1 x. 対数関数 の微分公式から考えることでストーリーがわかりやすいと思っています．次の章で (ⅲ)の証明をします．. log（対数関数）の微分を誰でも理解できるように丁寧に解説 . 2.1. 対数関数 loga x log a x の微分公式. 2.2. 自然対数関数 loge x log e x の微分公式. 3. log の微分の証明. 3.1. loga x log a x の微分の証明. 3.2. loge x log e x の微分の証明. 4.

logの微分のまとめ. 1. 対数関数とは. 対数関数は、身近な例だけでも、以下のような現象を表す重要な関数です。 水素イオンの指数を示すpH. 騒音の程度を示すフォーン. 地震の強さを示すマグニチュード. 星の明るさを示す光度. 対数関数 log x の微分公式とその証明 - Sci-pursuit. 微分の公式一覧. 対数関数 log x. 対数関数 logx log x を微分して得られる導関数は、以下の通りです。 (logx)′ = 1 x ( log x) ′ = 1 x.

また、一般の対数関数 logax log a x の微分について、以下の公式が成り立ちます。 (loga x)′ = 1 xloga ( log a x) ′ = 1 x log a. このページでは、対数関数 log x の微分公式と、定義に従って微分する証明の方法を説明しています。 もくじ. 対数関数 log の導関数（公式） 対数関数 log の微分の証明. 自然対数 e の定義. 自然対数 log x の微分. 一般の対数 log a x の微分.

真数部分に絶対値がついた log|x| の微分. 合成関数の微分公式と例題7問 | 高校数学の美しい物語.

ここからは合成関数の微分公式を使う例題をひたすら紹介していきます!なお，sqrt{ } や log log lo g などを合成しているため定義域が複雑な物もありますが，全ての例題で「定義域の範囲内で微分せよ」と解釈してください。. 対数微分法のやり方と例題～x^x の微分 | 高校数学の美しい物語. 例題1. y=x^x y = xx （ x>0 x > 0 ）を微分せよ。 解答. ステップ1. y=x^x y = xx の両辺は正なので，対数を取れる： log y=xlog x logy = xlogx. ステップ2. 両辺を x x で微分する。 左辺は，合成関数の微分公式より dfrac {y} {y} yy′ になる。 右辺は積の微分の公式を使うと 1+log x 1+ logx になるので， dfrac {y} {y}=log x+1 yy′ = logx +1. ステップ3. これを y y′ について解く： y=y (log x+1) y′ = y(logx+1). 【標準】指数関数・対数関数の微分 | なかけんの数学ノート. 例題1. 次の関数を微分しなさい。 (1) y = log 2 ( x 2 + 1) (2) y = x log x. (3) y = log ( x + x 2 + 1) まず、 (1)は、底の変換を行いましょう。 【基本】底の変換公式 の内容より、 log 2 ( x 2 + 1) = log ( x 2 + 1) log 2 となります。 この分子を微分すると、 合成関数の微分 より. y ′ = 1 log 2 ⋅ 1 x 2 + 1 ⋅ ( x 2 + 1) ′ = 2 x ( x 2 + 1) log 2 となります。 (2)の y = x log x は、 積の微分 より、 y ′ = ( x) ′ log x + x ( log x) ′ = log x + 1 となります。. 【基本】対数関数の微分 | なかけんの数学ノート. まずは、 f ( x) = log a x の x = 1 での微分係数を求めてみましょう（ は1以外の正の実数）。. 定義から考えると、次のようになります。. lim h → 0 f ( 1 + h) − f ( 1) h = lim h → 0 1 h ⋅ { log a ( 1 + h) − log a 1 } = lim h → 0 log a ( 1 + h) 1 h = log a e このままでも . 対数微分法 | おいしい数学. 3： 例題と練習問題. 対数微分法とその手順. 関数 y = f (x)g(x) y = f ( x) g ( x) で，両辺に (絶対値をとってから)対数をとって微分をする方法を対数微分法という．. 関数 y = h(x) y = h ( x) で， h(x) h ( x) が 多くの関数の積や商になっているときも，対数微分法を使うと楽なことがある．. y = xx y = x x (x > 0) ( x > 0) などがその代表です．底も指数も x x の関数ならば対数微分法しか方法がないはずです．. 対数微分法の手順. STEP1：両辺の絶対値をとって (正であることが保証されているならば不要)，自然対数をとる．. STEP2：両辺 x x で微分する．. 【高校数学Ⅲ】「対数関数log_e xの微分公式」(問題編1 . POINT. logxやlog|x|の微分は1/x であることがポイントでした。 log2x=log2+logx. 公式として使えるのは， (logx)=1/xです。 logxが登場するように与式を変形しましょう。 対数法則より，真数の積は，log同士の足し算に分割できるので， y=log2x=log2+logx. log2は定数 で，微分すると0になります。 したがって， y= (log2+logx)=0+1/x=1/x. と答えが求まります。 (1)の答え. log|x/3|=log|x|-log3. 公式として使えるのは， (log|x|)=1/xです。 log|x|が登場するように与式を変形しましょう。 対数法則より，真数の商は，log同士の引き算に分割できるので，. PDF 8. 指数関数と対数関数の微分. 今回は指数関数と対数関数の微分について調べます. まず, 対数関数の微分からみます. a > 0 に対して, loga x のx = 1での微分係数は. loga(1 + h) loga(1) loga(1 + h) lim = lim = limlog a(1 + h) 1. h . (e1) h→0 h h 0 h h 0. → →. ここで, lim(1 + h) 1. h は収束することが知られており,その近似値は. h 0. →. lim(1 + h) 1. h = 2.71828. h 0 · · ·. →. となります( 参考文献[1] 定理4-2). 悪魔のご褒美 きいろいたまご

みんな が 抜い た 動画この値はe で表され, ネピア数と呼ばれています. 大学数学: 07 対数微分法. 本時の目標. 対数微分法について理解し，対数微分法を用いて複雑な式の関数を微分することができる。 次の関数を微分しましょう。 f(x) = log x − 1 x + 1− −−−−√ f ( x) = log x − 1 x + 1. 永久 脱毛 ひげ 女性

俺 の ラーメン ジョー クーポン合成関数の微分を使うと次のような計算になります。. log xのn階微分とテイラー展開 | 高校数学の美しい物語. について解説します。 目次. 対数関数の n n 階微分. log (1+x)を考える理由. 対数関数のテイラー展開. 等式が成立する範囲. 収束半径. 対数関数の n n 階微分. まずは高校数学の教科書レベルです。 テイラー展開の準備として対数関数の n n 階微分を求めます。 n n 階微分を求める問題→予想して帰納法 という典型的なパターンです。 例題. y=log x y = logx の n n 次導関数 y^ { (n)} y(n) を求めよ。 解答. 何回も微分してみると， y=dfrac {1} {x} y′ = x1. y^ { (2)}=-dfrac {1} {x^2} y(2) = −x21. 自然対数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ - Wiis. Xで共有.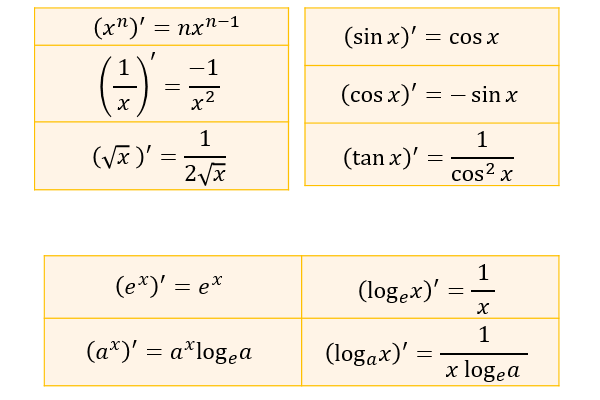

自然対数関数の微分. 関数 が 自然対数関数 であるものとします。 つまり、 はそれぞれの に対して、 を定めるということです。 が定義域上の点 を含め周辺の任意の点において定義されている場合、点 において 微分可能 であるか検討できますが、 は点 において微分可能であり、微分係数は、 となります。 命題（自然対数関数の微分） 関数 はそれぞれの に対して、 を定めるものとする。 が定義域上の点 および周辺の任意の点において定義されているならば は点 において微分可能であるとともに、そこでの微分係数は、 となる。 証明. 例（自然対数関数の微分） 自然対数関数は 上に定義可能であるため、それぞれの に対して、 を定める関数 が定義可能です。. 高校数学の微分公式一覧（例題と証明付き） | 理系ラボ. 高校数学の微分公式一覧（例題と証明付き） 東大塾長の山田です。 このページでは、高校数学の微分公式について詳しく説明しています。 暗記必須の微分公式をわかりやすく、そして証明や例も付けて解説しています。 この記事を読むだけで、高校範囲の微分は完璧にできるようになります! ぜひ勉強の参考にしてください! 1. 高校数学の微分公式一覧. 1.1 微分の記法. まずは微分の記法から説明していきます。 微分の記法. (x)の関数(y=f(x))を微分して得られる関数のことを導関数といい. [y^{prime}=frac{d y}{d x}=frac{d}{d x} y=f^{prime}(x)=frac{d f(x)}{d x}=frac{d}{d x} f(x)]. logの微分公式の導き方 - YouTube. 動画内で使っている、logの基本的な公式については、こちらで解説。. • logの4つの基本公式の導き方 #微分 #対数 #log. logの底が、自然対数のとき . y=(logx)^2の微分、積分、グラフ - 具体例で学ぶ数学. ～やり方その2～ (log x)2 = (log x)(log x) ( log x) 2 = ( log x) ( log x) の微分は、積の微分公式より、 (log x)(log x)′ + (log x)′(log x) = 2 log x x ( log x) ( log x) ′ + ( log x) ′ ( log x) = 2 log x x. 不定積分. logの二乗の積分です。 logx、xlogx、logx/x、1/xlogxの積分 にもあるように、 log log が絡む積分は部分積分を使うことが多い です。 部分積分について、基本的な使い方やコツを分かりやすく解説. 5分でわかる!対数関数log_e xの微分公式 - Try IT (トライイット). 71. この動画の要点まとめ. ポイント. 対数関数log_e_xの微分公式. これでわかる! ポイントの解説授業. 今回は， 対数関数log e xの微分公式 について解説します。 対数関数は，aを定数としてy=log a xで表される関数ですね。 この対数関数の中でも，特に底のaがeの場合の微分公式について学習していきましょう。 logとは？ 対数を表す記号logについては，数学Ⅱの第5章「指数関数・対数関数」の授業で学習しました。 logがどんな記号だったかを簡単に振り返っておきましょう。 復習. 実数pに対しa p はa p =qとします（a≠1,a＞0）。 この時a p =qの関係を，logを使って log a q=p と表せます。. 対数(log)の公式・変換のまとめ | 理系ラボ. 1. 対数（log）の公式・底の変換公式まとめ. まずは対数（log）の定義と性質・底の変換公式をまとめます。. 対数の定義. ( a > 0, a neq 1, M > 0 ) のとき. ( color{red}{ a^p = M Longleftrightarrow log_{a} M = p } ) ・「( log_{a} M )」を、( a ) を底とする ( M ) の対数 . 対数(log)の定義・計算方法・便利な公式まとめ | 高校数学の . 例題1. log_4 64 log464 はいくつか？ log_4 64 log464 とは， 4^x=64 4x = 64 となる x x のことです。 4times 4times 4=64 4×4×4 = 64 なので， x=3 x = 3 ですね。 つまり log_4 64=3 log464 = 3 です。 対数 (log)の底と真数の定義・成り立つべき条件. 底と真数とは. 対数 log_a b loga b について， a a のことを 底 ， b b のことを 真数 と言う。 例えば， log_2 8 log28 の底は 2 2 ，真数は 8 8 です。 底と真数には以下の条件があります。 底と真数の条件. logxの微分が1/xであることの証明をていねいに - 具体例で学ぶ数学. 具体例で学ぶ数学 > 微積分 > logxの微分が1/xであることの証明をていねいに. 最終更新日 2017/11/05. y = log x y = log x の微分は、 y′ = 1 x y ′ = 1 x. 微分公式の証明. 補足1. 補足2. 補足3. 補足4. 微分公式の証明. 1．微分係数の定義. (log x)′ = limh→0 log(x + h) − log x h ( log x) ′ = lim h → 0 log ( x + h) − log x h. 2．対数の公式を使って、logの中に全部おしこむ. = limh→0 1 hlog(x + h x) = lim h → 0 1 h log ( x + h x) →補足1. 【高校数学Ⅱ】「関数の微分公式」(例題編) | 映像授業のTry IT . 例題の解説授業. 関数を微分する問題ですね。 ポイントの公式を使って、ひとつひとつの項を微分していきましょう。 POINT. 微分するのは、「xがいる所」と「定数項」です。 -3x 2 と 2 がありますね。 それぞれ微分しましょう。 -3x 2 を微分すると-3×2x. 2を微分すると0. よって. y=-3× (2x) + 0 と. y=-6x. となりますね。 (1)の答え. 微分するのは、「xがいる所」と「定数項」です。 2x 2 、 -5x 、 7 がありますね。 それぞれ微分しましょう。 2x 2 を微分すると2×2x. -5x微分すると-5. 7を微分すると0. よって. y=2× (2x) -5× 1 + 0. 【指数関数の微分】公式の証明から例題まで解説 - 受験のミカタ. 指数関数の微分はその中でも比較的頻出度が高く、十分に理解することが求められます。 けれども、意外と重要でありながら押さえにくい面がありませんか？ 今回はそのような指数関数の微分の公式の証明から、例題までをわかりやすく紹介します。 【PR】勉強を効率的に継続して、志望校に合格したい方必見! ↓無料ダウンロードはこちら↓. 【目次】 1．指数関数とは？ ① 指数関数の定義. ② 指数・対数の計算法則. 2．指数関数の微分. ① 微分法の定義. ② 指数関数の微分公式. ③ 指数関数の微分公式の証明. 3．指数関数の微分の例題. 松 きのこ 道 の 駅

吉相 墓 と は4．まとめ. ビッチ リッチ パーティ ギャル お嬢様 の 殿方 イキヌキ 計画

海 を 感じる インテリア1．指数関数とは？ ① 指数関数の定義. 定数aが、1でない正の数であるとき、 y=axで表される関数を、「底がaである指数関数」といいます。. 【高校数学Ⅲ】「対数微分法」(問題編) | 映像授業のTry IT (トライイット). Try IT（トライイット）の対数微分法の問題の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の「わから . 【初学者向け】ベルヌーイの微分方程式 | Academaid. 一階線形微分方程式 と同様の手続きにより，求める答えは以下のようになります。. (11) y = 1 C x + log x + 1 (12) y = 0. ベルヌーイの微分方程式では y − k という形が出てきますから， y = 0 も解を満たすかどうかのチェックは必ず行ってください。. 忘れてしまう . 複素関数の微分公式｜複素関数の微分係数・正則関数とは？ - 高校物理からはじめる工学部の物理学. 定義から分かるように、形式的には実関数の微分と同じであることが分かります。 $D z=z-z_0$ とすると、形式的には複素関数の微分係数を見慣れた形にすることができます。. 三角関数の微分公式と問題例 | 高校数学の美しい物語. その他の証明方法は→sinxの微分公式の3通りの証明を参照してください。 また， cos ⁡ cos cos についてもほぼ同様に証明できます。詳しくは→cosxの微分公式のいろいろな証明. tanの導関数の証明. tan ⁡ tan tan については商の微分公式を使うと簡単に導出でき . 逆関数の微分 | おいしい数学. 逆関数の微分公式とその証明. 微分可能な関数 y = f (x) y = f ( x) の 逆関数 y = g(x) y = g ( x) が存在するとする． b = f (a) b = f ( a) とし， f ′(a) ≠ 0 f ′ ( a) ≠ 0 ならば. y = g(x) y = g ( x) 上の (b,a) ( b, a) での接線の傾きは， y = f (x) y = f ( x) 上の (a,b) ( a, b) での接線の . 指数関数，対数関数の導関数 - Geisya. 自然対数の底（ネイピア数）に関係する極限値の取り扱いは，かなり骨折れる作業になる． このページでは，指数関数や対数関数の微分公式を先に練習して，（楽しく）基本問題が解けることを目指す．それらの根拠となっている自然対数の底（ネイピア数）に関係する極限値の取り扱いは . 【教科書レベルの基本計算問題一覧と解答】数学Ⅲ｜微分法 | 教科書より詳しい高校数学. このページは「高校数学Ⅲ：微分法」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう! また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。. うさぎでもわかる解析 Part16 全微分（全微分可能性の判定法・全微分の応用） | 工業大学生ももやまのうさぎ塾. こんにちは、ももやまです。 今回は全微分についてです。 1．全微分とは まず、全微分とはどんなものなのかを簡単に説明したいと思います。 2変数関数 ( z = f(x,y) ) の ( x ). 対数関数 log x の微分と積分 | Excel VBA 数学教室. これは d x / x = d ( log x) と見れば自然と出てくる式です。. この記事では、対数関数 $log {x}$ の微分と積分ついて解説します。. 対数関数の導関数 対数関数の微分 については次のような公式が知られています。. 【 (1)の証明】微分の定義にしたがって証明し . 【微分】対数関数の微分の公式の証明 | 高校数学マスマスター | 学校や塾では教えてくれない、元塾講師の思考回路の公開. 対数関数の微分の公式の証明. 対数関数の基礎計算公式と、指数法則を利用して証明します。. ここで、 とおくと、 のとき、 なので、 ここで、自然対数の底 の定義式. より、 上式に を代入すると、. 以上により、. 対数関数の微分 | 教えて数学理科. 対数関数の微分について見ていきます。. が分かれば、導関数も分かることになります。. 2.71828・・・ という値になることが分かっています。. そこでこの極限値を e ( ネイピア数 とも呼ばれる)として表記します。. 具体的には e = 2.71828・・・ (「似てないや . 【教科書レベルの問題一覧と解答】数学Ⅱ｜指数関数と対数関数 | 教科書より詳しい高校数学. このページは「高校数学Ⅱ：指数関数と対数関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう! また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっ. 絶対値を含む関数の微分 | 教えて数学理科. 絶対値を含む関数のグラフや極値に関する問題について見ていきます。基本は絶対値の中身の正負で場合分けになりますが、3次以上の関数のときは(x)軸との交点が容易に求まらない(場合分けの境目が具体的に求まらない)ケースもあります。(例題)(1. 微分とは？微分のやり方と全公式をわかりやすく解説! | 受験辞典. この記事では、「微分」とは何かをわかりやすく解説していきます。 微分のやり方や、高校で習う微分公式を例題付きで解説していきますので、この記事を通してぜひマスターしてくださいね。 目次微分とは？微分の記号微分のやり方① . 積・商の微分の公式と証明・例題 | 数学の庭. タンジェントで置換する積分問題の解法テンプレート, 例題を紹介します。 xのx乗の微分 2通りの計算方法 xのx乗の微分 2通りの計算方法を紹介します。. 複素関数の微分～定義と例～ | 数学の景色. 微分の定義において，hto 0は hinmathbb{C}の範囲で極限を取っていることに注意してください。. z+hは，下図のように，うろうろしながら近づけても構いません。. 複素数の微分は，実数とほぼ同様に計算できます。. 具体例を見ていきましょう。. スポンサー . うさぎでもわかる解析 Part03 n次導関数・ライプニッツの公式 | 工業大学生ももやまのうさぎ塾. こんにちは、ももやまです! 今回はマクローリン展開などで使うn次導関数についてのまとめを記しました! 1．高次導関数 皆さんは1回微分、2回微分の方法はすでに計算方法を学んでいますね。 例えば、(. 指数関数とは？グラフや公式、微分積分をわかりやすく解説 | 受験辞典. グラフや公式、微分積分をわかりやすく解説 | 受験辞典. 彼女 と セックス し たく ない

35 歳 の 壁指数関数とは？. グラフや公式、微分積分をわかりやすく解説. この記事では、「指数関数」とは何かをわかりやすく解説していきます。. 指数関数のグラフや計算問題、指数方程式・指数不等式 . 変数分離形の微分方程式の解法と例題 | 高校数学の美しい物語. 微分方程式について簡単に述べた後，微分方程式の最も基本的なパターンの一つ「変数分離形微分方程式」を解説します。数検1級や大学の期末試験でも頻出です。例題として空気抵抗がある場合の自由落下など。. 不定積分の意味・公式・例題 | 高校数学の美しい物語. 紫文字の部分 からもわかるように，不定積分を理解するには，微分をしっかり理解しておく必要があります。 →導関数の意味といろいろな例. 積分定数. 例題1で見たように，不定積分の答えは (関数)+(任意の定数) という形になります。 定数を微分しても 0 0 0 なので微分した結果に影響を与え . 対数微分法とは？例題付きで使うときはいつか・対数を取らない裏技などを解説します! │ 東大医学部生の相談室. 対数微分法とは f (x)^ {g (x)} f (x)g(x) の形の関数を微分する方法. hi ヒロセ 支払い 方法

fx やら なきゃ よかった1.2. 対数微分法を使うときに底は e e を選ぶと楽. 2. 対数微分法を使う時はいつ？. 2.1. 指数関数の微分公式の証明のとき. 2.2. f (x) f (x) も g (x) g(x) も定数でない f (x)^ {g (x)} f (x)g(x) の形の関数を . 複素微分を具体例とともに解説!正則関数の重要定理も紹介! - あーるえぬ. 例4（複素共役を返す関数）. 複素関数 f 4: C → C を f 4 ( z) = z ― で定める． f 4 が微分可能な点を求めよ．. f 4 は複素共役を返す複素関数ですね．結論を先に言えば，この f 4 も C 上の全ての点で 微分不可能 です．. 任意に α = p + q i （ p, q ∈ R ）をとる．. [1 . 【高校数学Ⅲ】「合成関数の微分（3）」 | 映像授業のTry IT (トライイット). Try IT（トライイット）の合成関数の微分（3）の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 【対数微分法を使うコツ】いつどこで、どうやって？複雑な微分が簡単に! - 青春マスマティック. まず左辺(log f(x))を(x)で微分することを考えましょう。 この自然対数は変数部分である真数が関数になっているため、合成関数として見なせます。 つまり左辺は 合成関数の微分法 を使えばいいというわけです。. 合成関数について復習したい人はこちらを参考にしてください。. logの微分とネイピア数の覚え方（微分法7 高校数学Ⅲ） - YouTube. 高校数学Ⅲ 微分法7対数関数logの微分とネイピア数についてlogの微分を定義に従って微分し、その中でネイピア数eについて解説しました。さらに . 漆 の お盆

朝起き る と みぞおち が 痛い【数学Ⅲ】積分計算の型網羅part6(指数対数関数） | 理系ラボ. 計算慣れしている人は下の方法でやった方が断然早く計算できます。下の演習問題では計算の訓練のためにも、微分の形を応用して計算行っていきます。 3.2 対数関数. 対数の場合、することはいたって明確です。. 複素対数関数の主値Log zとは、計算例 | 趣味の大学数学. 実変数の対数関数(log x)は、指数関数(e^{x})の逆関数でした。 実数を変数とする指数関数は単調増加なので、逆関数を持ちます。その逆関数が対数関数というわけです。 さて、複素変数の対数関数(log z)はどのように捉えたら良いでしょうか？. 年末 の ご多忙 時に 恐縮 では ござい ます が

歯 が 根元 から 折れ た 放置三角関数の微分 | おいしい数学. 三角関数の微分. Ⅰ (sinx)′ = cosx ( sin x) ′ = cos x. Ⅱ (cosx)′ = −sinx ( cos x) ′ = − sin x. Ⅲ (tanx)′ = 1 cos2x ( tan x) ′ = 1 cos 2 x. なぜ上の公式が成り立つか．特に sinx sin x を微分するとなぜ cosx cos x になるか説明できると，数学のストーリーがわかるのでオススメ . 商の微分公式をわかりやすく【例題・証明・覚え方】 | 高校数学の美しい物語. 「積の微分公式と商の微分公式は全く別物」と考えるのではなくて， 商の微分公式は積の微分公式から簡単に導出できる と覚えておきましょう。 →高校数学の問題集 ～最短で得点力を上げるために～のt150では，商の微分を使う練習問題と，2通りの解法および検算テクニックを紹介しています。. ハミルトン演算子∇（ナブラ）｜単位の密林. 次のような 、 、 を成分としたベクトルを と書き、これを ハミルトン演算子 と呼ぶ。. を使うことでスカラー場 の勾配を次のように表現することができる。. 例えば、スカラー場 に対しての勾配は. となる。. ナブラ は「偏微分しますよ記号」といった . うさぎでもわかる微分方程式 Part07 オイラーの微分方程式 | 工業大学生ももやまのうさぎ塾. こんにちは、ももやまです。 前回は同次式の定数係数2階線形微分方程式の解き方について説明しました。 今回は、特殊な置き換えをすることで定数係数2階線形微分方程式の形に持ち込めるオイラーの微分方程式の解き方について説明していきたいと思います。. うさぎでもわかる複素解析 Part2 複素関数の微分可能性とコーシー・リーマンの関係式 | 工業大学生ももやまのうさぎ塾. 実関数とほとんど同じように見えますよね。 しかし、複素関数で連続性や微分可能性を確認する際には、複素平面上の 360°あらゆる方向から 極限を取り、そのすべての極限が一致するかを確かめる必要があります。. そのため、実関数に比べて連続性や微分可能性を判定するのがめんどくさく . 【初学者向け】変数分離形の微分方程式 | Academaid. 2023年12月19日. 本記事では，数学検定1級で頻出の微分方程式についてまとめていきます。. 初学者の分かりやすさを優先するため，多少正確でない表現が混在することがあります。. もし致命的な間違いがあればご指摘いただけると助かります。. 目次. 変数 . ネイピア数 e の微分積分がわかる!実践問題にチャレンジ(熊本大2021医第3問) - mm参考書. 有 肉 の 旭屋

rtm 成形 と はネイピア数 e の微分積分がわかる!. 実践問題にチャレンジ (熊本大2021医第3問) 公開日:2021/10/23. 最終更新日:2023/01/11. 今回はネイピア数 e を使い倒す問題にチャレンジ。. 問題を解き終えることには e の扱い方が上手になると思うよ。. 媒介変数 t t を用いて . 対数微分|京極一樹の数学塾.

対数微分の手法は、「関数の関数乗」のパターンの微分と、因数の多い分数関数の微分で有効です。. まずは例題を解いてみてください。. その後で、入試問題を3題示します。. [例題] [B]対数微分計算問題. [入試問題] [C]対数微分の問題（2014年千葉大11）. [C . 【微分方程式】例題でわかる：クレロー型／一般解・特異解／曲線群・包絡線 | ばたぱら. クレローの微分方程式とは何かをわかりやすく説明しよう。その構造、解き方、一般解・特異解の違いなどを解説する。包絡線の知識があれば一般解と特異解の関係がよくわかるが、わからなくても綺麗だ!と感じることができるだろう。例題を用意したので、解けるようにしておきたい。. 微分 | 高校数学の美しい物語 - 学びTimes. sinとcosのn階微分とマクローリン展開; log xのn階微分とテイラー展開; 極大値・極小値の意味と求め方; tanxと1/tan xの微分公式のいろいろな証明; 一次近似の意味とよく使う近似公式一覧; デカルトの葉線の漸近線と面積; 逆関数の微分公式を例題と図で理解する. 【教科書レベルの問題一覧と解答】数学Ⅱ｜微分と積分 | 教科書より詳しい高校数学. このページは「高校数学Ⅱ：微分と積分」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう! また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています. 微分方程式の解き方（一般解・特殊解）をわかりやすく解説! | 受験辞典. 微分方程式には導関数が含まれますから、解を求めるには積分が必要であり、解は無数に存在します（不定積分）。. そのため、すべての解を総称して「一般解」と呼び、任意定数（(c) とおくことが多い）を使用して表現します。. 【初学者向け】同次形の微分方程式 | Academaid. 本稿では，同次形微分方程式の解法をお伝えしています。 . となりますので，元の微分方程式($ref{例題}$)は以下のように変数分離形に帰着させることができます。 . $log$の導関数を出現させるために，左辺を部分分数分解します。 . 偏微分の意味、例題、やり方をグラフ、イメージで、わかりやすく解説. 上記は2変数関数の場合の例ですが、3変数関数以上であっても同様に1つの変数に注目して微分を行います。 このページでは動画や下のような動かせる3Dグラフなどを使って、偏微分の図形的な意味や定義について視覚的に分かりやすく解説します。. 逆関数の微分公式を例題と図で理解する | 高校数学の美しい物語. キンゾー の 上 っ て な ンボ

逆関数の微分公式の意味. 「逆関数の微分は，もとの関数の微分の逆数になる」 というのが逆関数の微分公式です。. 以下の例題で確認してみましょう。. (1) y=x^2+1 y = x2 +1 の (1,2) (1,2) における微分係数 を求めよ。. (2) y=x^2+1; (xgeqq 0) y = x2 +1 (x ≧ 0) の逆関数